What is Image Processing?

The term image processing refers to the use of certain mathematical operations to enhance, manipulate or extract useful information from an image. This includes operations designed to change how the image appears, as well as operations designed to change the properties of the signal that underlies the image. As an example, if we were to take every voxel in the image and multiply their value by 5, we would get an image that would appear brighter than the original image when using the same colourmap, as shown in Fig. 1.

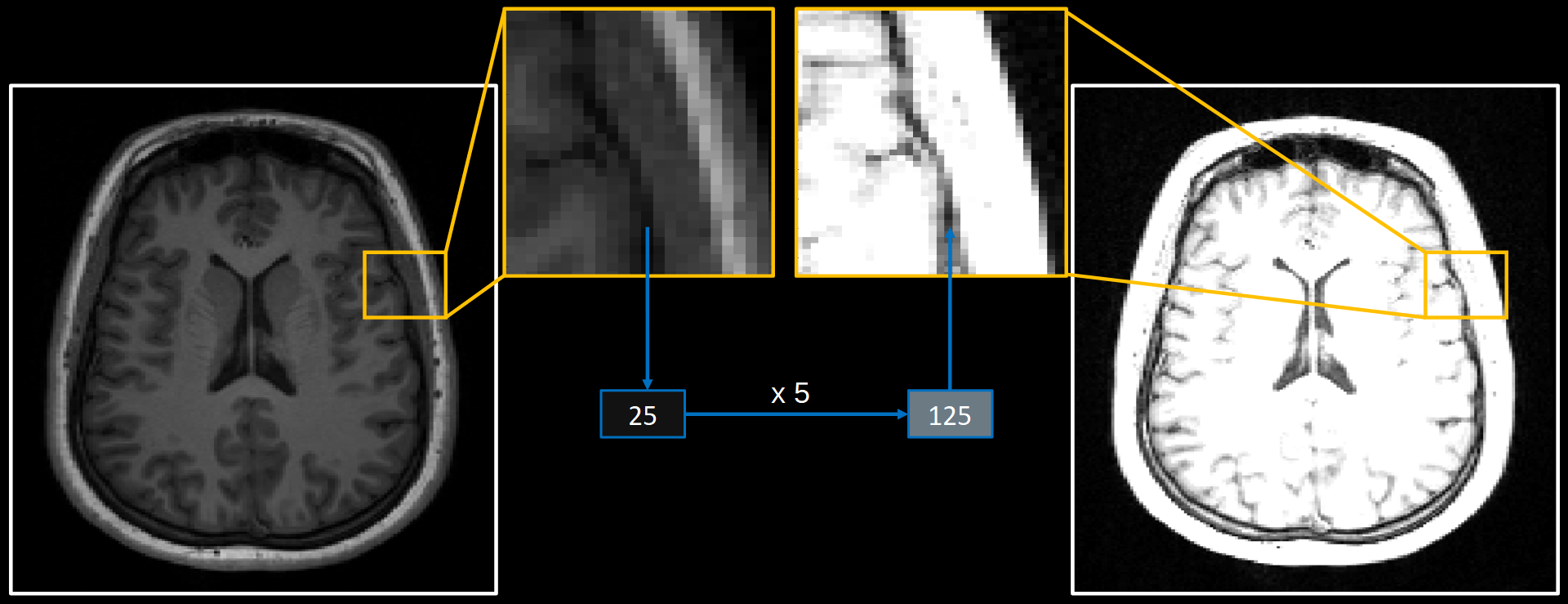
Fig. 1 Example of multiplying each voxel value by 5 to increase the brightness of an image using a fixed colour map.

Alternatively, we could leave the values unaltered but instead move each voxel to a different location in the image. For instance, moving each voxel 15 steps to the right would shift the location of the brain relative to the bounding-box of the image, as shown in Fig. 2.

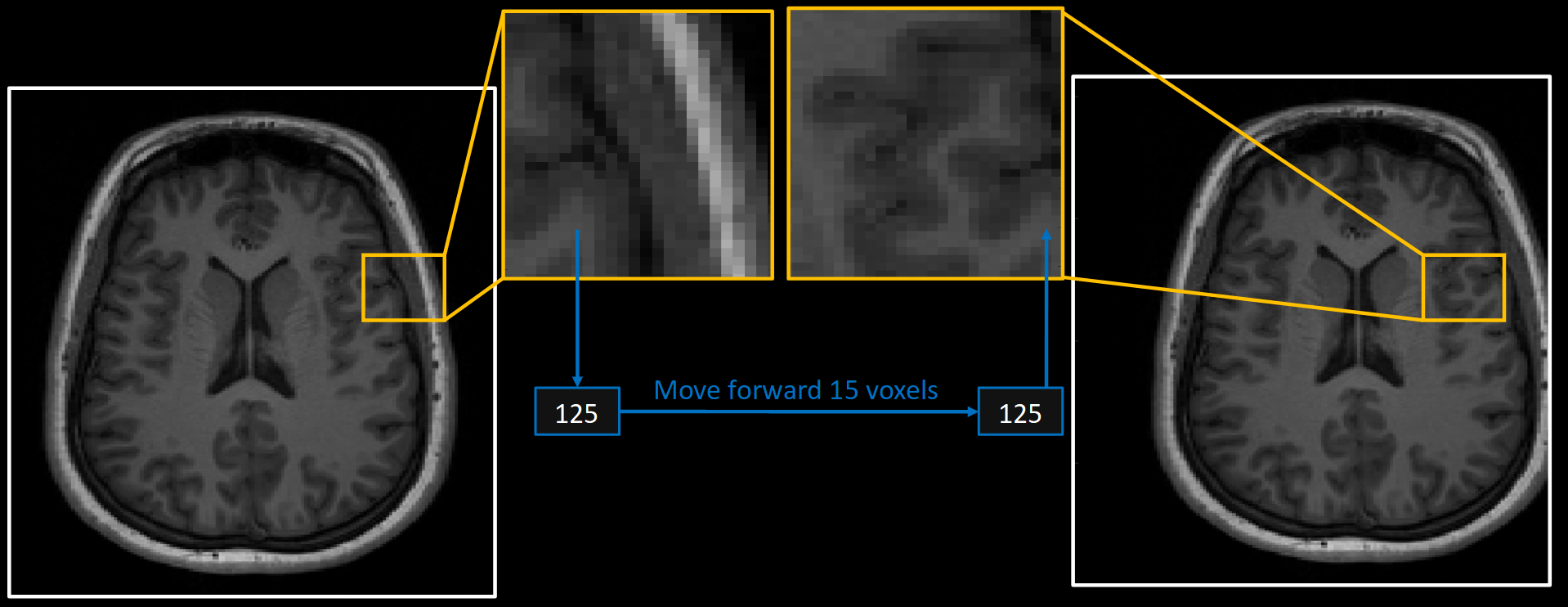
Fig. 2 Example of moving each voxel value to shift the location of the brain relative to the bounds of the image.

Both of these examples illustrate how we alter images in different ways by simply changing voxel values using some criteria. Sometimes we apply changes identically to each voxel and sometimes those changes depend on the voxel values themselves. Either way, the image is altered in some fashion to suit our needs. From this we can define two broad categories of transformations. Those which move the voxel values within the image can be classed as spatial transformations, whereas those which change the voxel values without moving them can be classed as image filters.

Spatial Image Transformations

Generally speaking, processing steps that move voxel values are concerned with how the voxel coordinates map onto the anatomy of the brain. The reason this is important is because a computer has no knowledge of anatomy. All the computer knows about are the voxel values and their coordinates within the data matrix. In order to derive any meaning from analysing an image, we have to make sure there is some meaningful correspondence between these coordinates and the anatomy of the brain.

As an example, if we took two structural MR images straight from the scanner and selected voxel coordinates \(\left[104, 167, 88\right]\), it is very unlikely that this voxel would correspond to the same anatomical location in both images. If we were to compare the voxel values from these coordinates across the two images then the comparison would be largely meaningless because of this lack of anatomical agreement. In order for there to be any meaningful connection between images, we need to spatially transform one of them by moving the voxel values around so that the same coordinates correspond to the same anatomical locations. This is illustrated in Fig. 3.

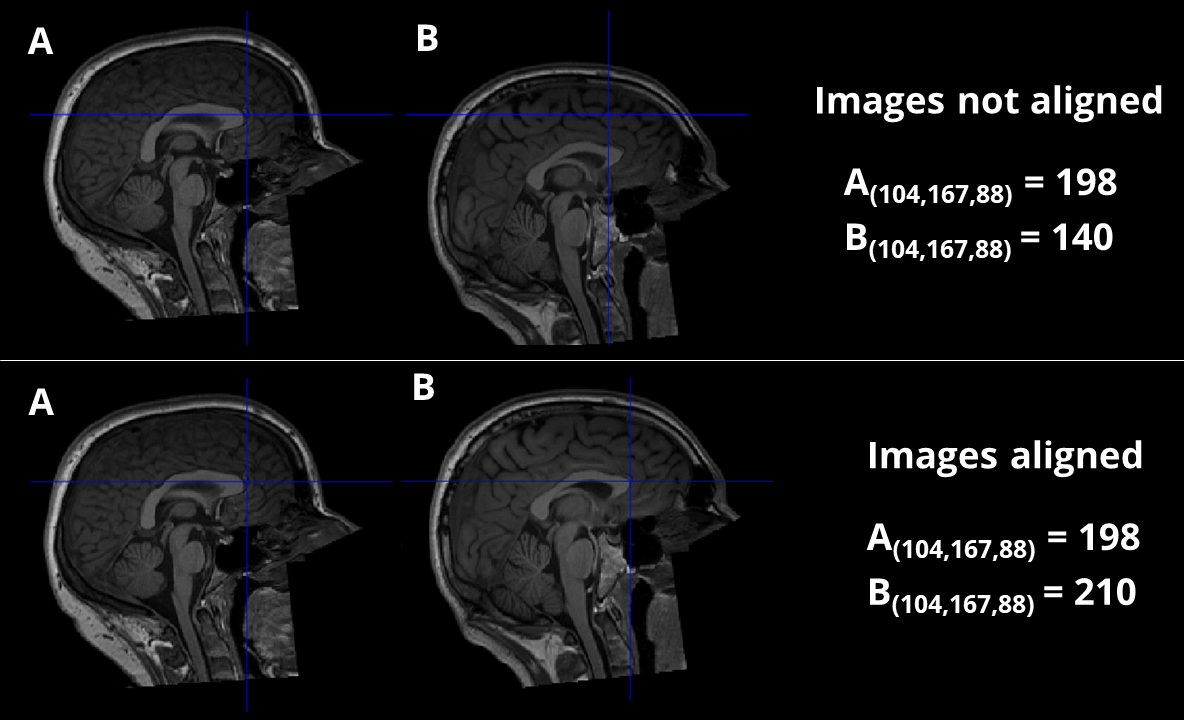
Fig. 3 Illustration of how the same coordinates across two images are meaningless unless there is anatomical alignment between them. In the top row, the images are not aligned and thus the voxel values derived from the same coordinates are not useful because they correspond to different anatomical regions. In the bottom row, the images are aligned and thus voxel values from the same coordinates can be meaningfully compared.

Image Filtering

By comparison, processing steps that alter the voxel values without moving them are concerned with enacting some meaningful change to the signal that underlies the image. Unlike spatial transformations, these forms of processing have little care for what they make the image look like. Rather, the changes are performed in an attempt to improve the quality of the data, or to enhance/remove certain features of the image. An important thing to remember with filtering is that the quality of the data and the quality of the image are not necessarily the same thing. Many filtering steps can make an image look worse, but actually improve the quality of the numeric data that underlies the image. An example of this would be the Gaussian filter, which makes the image look blurrier but actually improves the data by reducing noise. Examples of filtering operations and their visual effects are shown in Fig. 4.

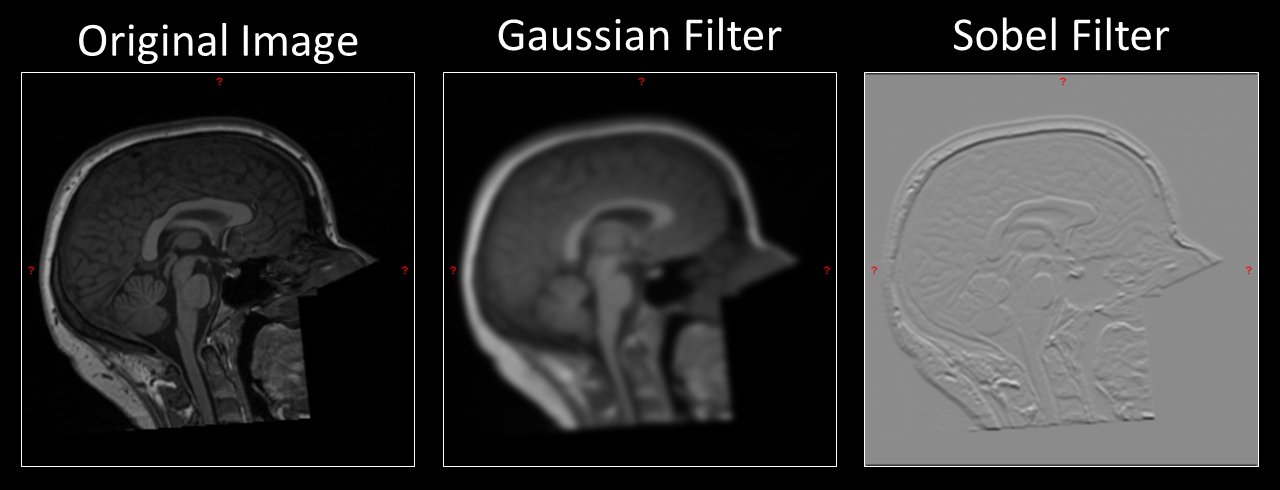
Fig. 4 Example of both a Gaussian and Sobel filter applied to an anatomical MR image. In both cases, the filter makes the image look subjectively worse. However, useful properties of the signal that underlies the image have been enhanced in each example.